FoxCalculators - Kostenlose Taschenrechner online!

Exponentialer Zerfall / Wachstum ist in der Mathmatik sehr nützlich. Der exponentielle Zerfall tritt auf, wenn die Wachstumsrate negativ ist. Das exponentielle Wachstum auf dieselbe Weise tritt auf, wenn die Wachstumsrate des Werts einer mathematischen Funktion proportional zum aktuellen Wert der Funktion ist.

Die Formel für ein exponentielles Wachstum einer Variablen x an der (positiven oder negativen) Wachstumsrate R, da die Zeit t in diskreten Intervallen eingeschaltet ist (dh bei ganzzahligen Zeiten 0, 1, 2, 3, ...), ist < b> x _{t = x 0 (1 + R) ^{t .}}

wobei x _{0 der Wert von x zum Zeitpunkt 0 ist. Wenn der R negativ ist, ist der Exponentialverfall, wenn das R positiv ist, ein exponentielles Wachstum. Zum Beispiel bewirkt die Wachstumsrate von R = 5% = 0,05, der von einem ganzzahligen Zeitwert der Zeit zur nächsten Ganzzahl führt, dass x zum zweiten Mal das 1,05-fache sein, was es zum vorherigen Zeitpunkt war.}

Zum Beispiel wird R = -0,5, der Graphen abnimmt (Abfall). Jedes Mal, wenn T um 1 erhöht wird, nimmt x _{t auf die Hälfte des vorherigen Werts ab.}

Wenn R = 1 ist, wird die Grafik wachsen. Jedes Mal, wenn t um 1 erhöht wird, erhöht sich x _{t um einen Faktor von 2.}

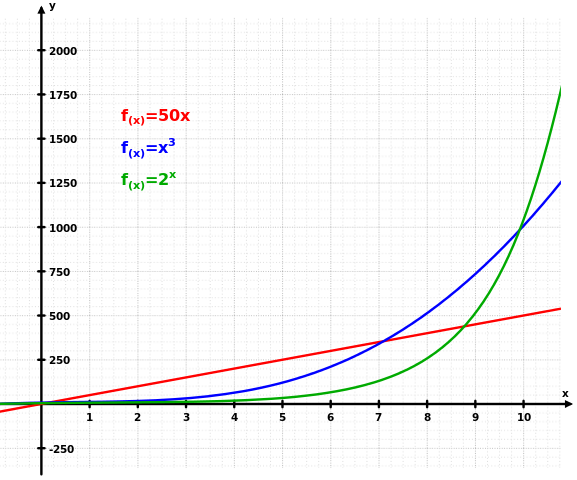
Die Grafik zeigt, wie exponentielles Wachstum (grün) sowohl lineares (rotes) als auch kubisches (blaues) Wachstum übertrifft.