Eigenvectoren und Eigenwerbsberechnung

Regular Matrix A =
Identity Matrix I =
Scalar Matrix(Z=c×I)
c =
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigen Value (c2) =
Eigen Value (c1) =
c1 in Eigen Vector x1 value =
c2 in Eigen Vector x1 value =
c1 in Eigen Vector x2 value =
c2 in Eigen Vector x2 value =

Ein Eigenvektor einer quadratischen Matrix A ist ein Nicht-Null-Vektor V, wenn ein V = λ V, der λ als Eigenwert von a entsprechend v genannt wird.

Alle Eigenwerte und Eigenvektoren erfüllen die Gleichung AX = λx für eine bestimmte quadratische Matrix A.

Die Online-Eigenevektoren und der EigenValues-Rechner können | A |, Singular Matrix (A - C × I), Spuren eines eignen Werts der Matrix A

Zum Beispiel

Für Matrix

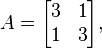
der Vektor

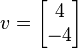
ist ein Eigenvektor mit Eigenwert 2.

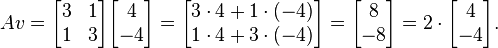
Auf der anderen Seite der Vektor

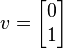
ist nicht einen Eigenvektor, da

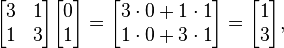
Und dieser Vektor ist kein Vielfaches des ursprünglichen Vektors v.

Eigenvectoren und Eigenwerbsberechnung
Empfehlung Taschenrechner Luftgeschwindigkeitslöser erfassen Gallonen pro Stunde Kraftstoffrechner Fließwandlerrechner Luftkanalflussrechner Wärmerückgewinnungsrechner Volumeneinheit-Konverter Drehmoment zum PS-Konverter Windleistungsrechner Hydraulikdurchmesser Solver. Rauschkriteriumrechner Geschwindigkeitsumrichter Luftkanal-Velocity-Rechner Luftstromkopfverlustrechner Kapazität des Erdgasrohrs Rechner Elektromotorenrechner