Eeigener Vektor, Eigenwert 3x3 Matrixrechner

 
Regular Matrix A =
Scalar Matrix (Z=c×I)
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigenvalue of c3 =
+ i
 
Eigenvalue of c2 =
+ i
Eigenvalue of c1 =
+ i
c3 in Eigenvector (x,y,z) values =
c2 in Eigenvector (x,y,z) values =
c1 in Eigenvector (x,y,z) values =

Ein Eigenvektor einer quadratischen Matrix A ist ein Null-Null-Vektor-V-Vektor Das ist: a v = λ v

(Da diese Gleichung nach der Multiplikation von V verwendet, beschreibt er einen rechten Eigenvektor.) Die Zahl λ wird als Eigenwert von a entsprechend v genannt.

Alle Eigenwerte und Eigenvektoren erfüllen die Gleichung AX = λx für eine bestimmte quadratische Matrix A.

Einfacher Matrixrechner zur Berechnung des Eigenwerts und des Eigenvektors einer 3x3-Matrix. Geben Sie die Werte der 3x3-Matrix ein und klicken Sie auf die Schaltfläche Berechnen.

Spur

Die Spur, TR (a) einer quadratischen Matrix A ist die Summe seiner diagonalen Einträge. Während Matrix Multiplikation nicht wie oben erwähnt ist, ist die Spur des Produkts von zwei Matrizen unabhängig von der Reihenfolge der Faktoren:

tr (ab) = tr (ba).

Dies ist unmittelbar von der Definition von Matrix Multiplikation:

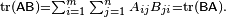
Außerdem ist die Spur einer Matrix gleich dem seiner Transponierung, d. H.

tr (a) = tr (a t ).

Eeigener Vektor, Eigenwert 3x3 Matrixrechner
Empfehlung Taschenrechner Luftgeschwindigkeitslöser erfassen Gallonen pro Stunde Kraftstoffrechner Fließwandlerrechner Luftkanalflussrechner Wärmerückgewinnungsrechner Volumeneinheit-Konverter Drehmoment zum PS-Konverter Windleistungsrechner Hydraulikdurchmesser Solver. Rauschkriteriumrechner Geschwindigkeitsumrichter Luftkanal-Velocity-Rechner Luftstromkopfverlustrechner Kapazität des Erdgasrohrs Rechner Elektromotorenrechner