MATRIX-Rechner umsetzen




 
Result:
A Transpose =

In der linearen Algebra ist die Transponierung einer Matrix A eine andere Matrix A t (auch ein ', a tr , t a oder < SUP> T ) erstellt durch eines der folgenden äquivalenten Aktionen:

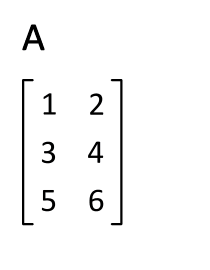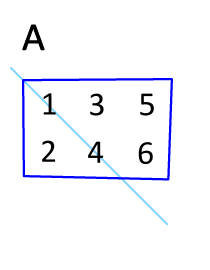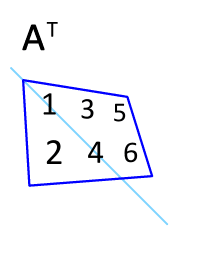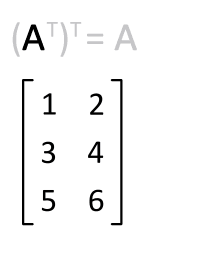
Der transponente matrixrechner Um die Matrix A umzuwandeln, um die Matrix ein t umzusetzen

Der Rechner gelten für Matrizen 3x2,3x3, 3x1,2x3, 1x3, 2x2, 2x1 und 1x2, um die Matrix A umzusetzen.

Die unteren Fig. 12 zeigt, wie man sich umsetzt:

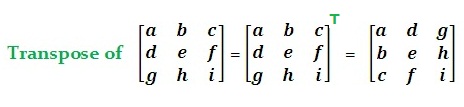
Transpose Matrix

MATRIX-Rechner umsetzen
Empfehlung Taschenrechner Luftgeschwindigkeitslöser erfassen Gallonen pro Stunde Kraftstoffrechner Fließwandlerrechner Luftkanalflussrechner Wärmerückgewinnungsrechner Volumeneinheit-Konverter Drehmoment zum PS-Konverter Windleistungsrechner Hydraulikdurchmesser Solver. Rauschkriteriumrechner Geschwindigkeitsumrichter Luftkanal-Velocity-Rechner Luftstromkopfverlustrechner Kapazität des Erdgasrohrs Rechner Elektromotorenrechner