FoxCalculators - Kostenlose Taschenrechner online!

In der Mathematik ist eine fortgesetzte Fraktion ein Ausdruck, der durch einen iterativen Prozess der Darstellung einer Zahl als Summe seines ganzzahligen Teils und der Kehrleitung einer anderen Zahl erhalten wird, und schreibt dann diese andere Zahl als Summe seines ganzzahligen Teils und einem anderen Kehrwert und so auf. In einem endlichen fortgesetzten Fraktion (oder terminierter fortgesetzter Fraktion) wird die Iteration / Rekursion nach endlich vieler Schritte unter Verwendung einer Ganzzahl anstelle eines weiteren anhaltenden Fraktionen beendet. Im Gegensatz dazu ist ein unendlicher anhaltender Fraktion ein unendlicher Ausdruck. In beiden Fällen müssen alle Ganzzahlen in der Sequenz, außer dem ersten, positiv sein. Die Ganzzahlen AI werden als Koeffizienten oder Bedingungen der anhaltenden Fraktion bezeichnet.

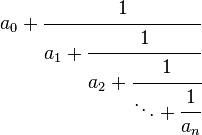
Eine endliche fortgesetzte Fraktion, wobei n eine nicht negative Ganzzahl ist, ein _{0 ist eine ganze Zahl, und AI ist eine positive ganze Zahl, für i = 1, ..., n.}

Fortsetzungsfraktion ist ein unendlicher Expression, der durch Schreiben einer Zahl als Summe seines ganzzahligen Teils und des Kehrens einer anderen Zahl und erneut der Summe der Ganzzahl der anderen Zahl und einem anderen wechselseitigen usw. ermittelt wird. Der fortgesetzte Bruchrechner drückt einen einfachen Fraktion aus, wie BO; B1, B2, ..... BN