Dreiecktheorems-Rechner |
| A = | |
| B = | |
| C = | 0 |
Der Triangle-Theorems-Rechner, um die Eigenschaften eines Dreiecks anhand anderer Eigenschaften eines Dreiecks zu finden.
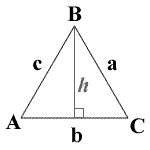
A = Seite A, B = Seite B, C = Seite c
A = Winkel A, B = Winkel B, C = Winkel C, K = Bereich, P = Perimeter
Manchmal konnte man AAA ASA SAS AAS SSS sehen, sie Bedeutungen:
AAA = Winkel, Winkel, Winkel
ASA = Winkel, Seite, Winkel
SAS = Seite, Winkel, Seite
AAS = Winkel, Winkel, Seite
SSS = Seite, Seite, Seite
Für EXMAPLE, zu SAS: Bei zwei Seiten und der Winkel zwischen diesen Seiten finden die restlichen Seiten und Angles.c = 3, B = 60 Grad, A = 6:
Verwenden Sie zum Berechnen a, verwenden Sie die folgende Formel: Arccos (b 2 + c 2 - a 2 ) / 2bc. Wenn Sie A, B und C für ihre Werte ersetzen, erhalten Sie Arccos ((60 2 + 6 2 - 3 2 ) / (( 2 * 60 * 6)), was 90.00005 ° entspricht.
Da die Winkel eines Dreiecks bis zu 180 ° Summieren summieren müssen, muss C die Summe aller drei Winkel entsprechen.
180 - 3 = 89.999955
89.99995 - 60 = 29.99995
Die Messung des dritten Winkels beträgt 29.99995 °.
Berechnung von K:
Um k zu berechnen, müssen Sie zunächst s finden. Um s zu finden, verwenden Sie die folgende Formel: S = (A + B + C) / 2.
(A + B + C) = 14.19616 und 14.19616 / 2 = 7.09808, S = 7.09808.
Nun, da Sie S gefunden haben, können Sie mit der Berechnung des Bereichs beginnen. Die Formel zur Berechnung des Bereichs eines Dreiecks ist
K = √ (s * (S-A) (S-B) (S-C)).
Stecken Sie zuerst Ihre seitlichen Längenwerte in die Formel: K = √ (7.09808 * (7.09808-6) (7.09808-5.19615) (7.09808-3).
Berechnen Sie anschließend alle Berechnung aller Werte in den Klammern:
K = √ (7.09808 * 1.09808 * 1.90193 * 409808).
Danach mehrere alle Zahlen zusammen: √ (60.7505).
Finden Sie schließlich die Quadratwurzel des Ergebnisses für Ihre Antwort: K = 7.79426 m 2 .
Berechnen von P:
Um p zu berechnen, fügen Sie alle Seiten zusammen: 6 + 5,19615 + 3 = 14.19615 m.p = 14.19615 m.
Sprachauswahl:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.