Rechter Kite-Rechner

Select data you know.

 












 
Significant Figures >>> 

Alle Kites sind tangentiale Quadrilaterals , was bedeutet, dass sie 4 einseitige Figuren sind, in denen ein Kreis (als incircle ) so eingeschrieben ist, dass jeder der vier Seiten den Kreis berührt an nur einem Punkt. (Grundsätzlich bedeutet dies, dass der Kreis zu jeder der vier Seiten des Kites tangentiert.)

Um einen Kreis grafisch (mit Kompass und gerade Rand) innerhalb eines Kites zu schreiben:

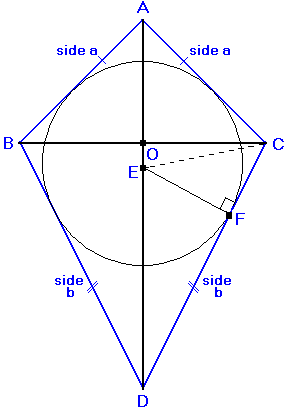
• Zeichnen Sie die Symmetrieachse an

• BISect eines der Nicht-Scheitelwinkel (B oder C) und erstrecken Sie diese Zeile, sodass sie die Zeilenanzeige an Punkt E erfüllt

• Zeichnen Sie von Punkt E ein senkrecht zu jeder der vier seiten.

• Zecken Sie den Kreis mit Punkt E als Mitte und Linie EF als Radius ein.

Beschreibt dies mathematisch :

• Winkel ACE = Winkel ECD = ½ Winkel ACD

• Winkel ACO = 90º - ½ Winkel BAC

• Winkel OCE = Winkel ACE - ACO

• OE = ½ Line BC x Tan (OCE)

• ae = oa + oe

• ed = ad -ae

• Winkel EDF = ½ Winkel BDC

• EF = SIN (EDF) x ed

Rechter Kite-Rechner
Empfehlung Taschenrechner Luftgeschwindigkeitslöser erfassen Gallonen pro Stunde Kraftstoffrechner Fließwandlerrechner Luftkanalflussrechner Wärmerückgewinnungsrechner Volumeneinheit-Konverter Drehmoment zum PS-Konverter Windleistungsrechner Hydraulikdurchmesser Solver. Rauschkriteriumrechner Geschwindigkeitsumrichter Luftkanal-Velocity-Rechner Luftstromkopfverlustrechner Kapazität des Erdgasrohrs Rechner Elektromotorenrechner