Rechner des rechten Dreiecks (Pythagoraner Theorem) Rechner

side a   side b   side c  
     
angle A   angle B   angle C  
     
Perimeter:    
Area:    
Inscribed Circle Radius:    
Circumscribed Circle Radius:    
Angle Bisector of a:    
Angle Bisector of b:    
Angle Bisector of c:    
Altitude of c:    
Median of a:    
Median of b:    
Median of c:    

Ein rechter Dreieck ist ein Dreieck, in dem ein Winkel ein rechtwinkliger ist.

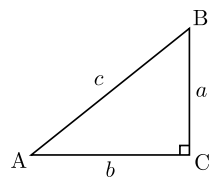
Die gegenüber dem rechten Winkel gegenüberliegenden Seite wird als Hypotenuse (Seite C in der Figur) bezeichnet. Die an den rechten Winkel angrenzenden Seiten werden Beine genannt (Seite B in der Figur). Seite A kann als die an den Winkel B angrenzende Seite identifiziert sein und den (oder dem gegenüberliegenden) Winkel A, während die Seite B die neben dem Winkel A angezeigte Seite ist und dem Winkel B gegenüberliegt.

Pythagoraner Theorem

C 2 = A 2 + b 2

Bereich

A × B / 2

Höhe von c (h)

A × B / C

Winkelbisseur von A

2 × B × c × cos (A / 2) / (B + C)

Winkelbissector von b

2 × A × c × cos (b / 2) / (a ​​+ c)

Winkelbisseeck von c (t c )

T C 2 = 2 × A 2 × B 2 / (a + b) 2

Median von a (m a )

M a 2 + 0,25 × A 2 .

Median von B (m b )

M B 2 = a 2 + 0,25 × b 2 .

Median von c (m c )

m c = c / 2

eingeschriebener Kreisradius

A × B / (A + B + C)

Umschickte Kreisradius c / 2

Rechner des rechten Dreiecks (Pythagoraner Theorem) Rechner
Empfehlung Taschenrechner Luftgeschwindigkeitslöser erfassen Gallonen pro Stunde Kraftstoffrechner Fließwandlerrechner Luftkanalflussrechner Wärmerückgewinnungsrechner Volumeneinheit-Konverter Drehmoment zum PS-Konverter Windleistungsrechner Hydraulikdurchmesser Solver. Rauschkriteriumrechner Geschwindigkeitsumrichter Luftkanal-Velocity-Rechner Luftstromkopfverlustrechner Kapazität des Erdgasrohrs Rechner Elektromotorenrechner