Konischer Krakatrechner |
| r1 = | |
| r2 = | |
| h = | |
| Units: | |
| s = | 0 |
| V = | 0 |
| L = | 0 |
| T = | 0 |
| B = | 0 |
| A = | 0 |
r1 = radius 1, r2 = radius 2, h = height, s = slant height, V = volume
L = lateral surface area, T = top surface area, B = base surface area,A = total surface area
Eine kreisförmige Formingan-obere Basis und eine untere Basis, die kreisförmig und parallel sind, kann aus einem rechten kreisförmigen Kegel gebildet werden, indem die Kegelspitze abgeschnitten wird.
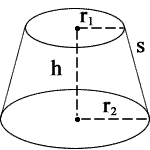
Beispielsweise an R 1 = 2, r 2 = 3, h = 4,
- .
Um S zu berechnen, verwenden Sie die folgende Formel: √ ((R 1 - R 2 ) 2 + h 2 ). Wenn Sie R 1 , r 2 , und h für ihre Werte ersetzen, erhalten Sie √ ((2 - 3) 2 + 4 2 ), was 4,12311 m entspricht.
Um V zu berechnen, verwenden Sie die folgende Formel: (1/3) πH (R 1 2 + R 2 2 + (R 1 + r 2 )). Wenn Sie R 1 , r 2 , und h für ihre Werte ersetzen, erhalten Sie (1/3) π * 4 * (2 2 + 3 2 + (2 * 3)), was 79,58701 m 3 entspricht.
Um L zu berechnen, verwenden Sie die folgende Formel: π * (R 1 + R 2 ) * s. Wenn Sie R 1 , r 2 , und s für ihre Werte ersetzen, erhalten Sie π * (2 + 3) * 4.12311, was 64.76566 m 2
Um t zu berechnen, verwenden Sie die folgende Formel: πr 1 2 . Wenn Sie R 1 für seinen Wert ersetzen, erhalten Sie π * 2 2 , was 12,56637 m 2 entspricht.
Um B berechnen, verwenden Sie die folgende Formel: πr 2 2 . Wenn Sie R 2 für seinen Wert ersetzen, erhalten Sie π * 3 2 , was 28.27433 m 2 entspricht.
Verwenden Sie zur Berechnung eines, verwenden Sie die folgende Formel: π (R 1 2 2 + (R < sub> 1 + r 2 ) * s). Wenn Sie R 1 , r 2 , und s für ihre Werte ersetzen, erhalten Sie π (2 2 + 3 2 + (2 + 3) * 4.12311), was 105.60636 m 2 ist.
Sprachauswahl:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.