Feste Oberflächenrechnungsrechner |
| a = | |
| r = | |
| Units: | |
| Surface Area = | 0 |
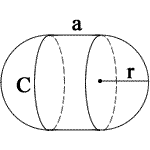 a = side length
a = side lengthr = radius
Rundkegelfläche
- .
Seitliche Oberfläche = πrs = πr√ (r 2 + h 2 )
Basisoberfläche = πr 2
Gesamtoberfläche
= L + b = πrs + πr 2 = πr (s + r) = πr (r + √ (R 2 + h 2 ) )
Kapseloberfläche
- .
Oberfläche = 2πr (2R + a)
Kreiszylinderoberfläche
- .
Top-Oberfläche = πr 2
Bodenfläche = πr 2
Gesamtoberfläche
= L + t + b = 2πrH + 2 (πr 2 ) = 2πr (H + R)
Würfeloberfläche
- .
Oberfläche = 6A 2
Konische Krümeloberfläche
- .
Seitliche Oberfläche
= π (R 1 + R 2 ) s = π (R 1 + R 2 ) √ (( R 1 - R 2 ) 2 + h 2 )
Top-Oberfläche = πr 1 2
Basisoberfläche = πr 2 2
Gesamtoberfläche
= π (R 1 2 2 + (r 1 * r 2 ) * s)
= π [r 1 2 2 2 + (r 1 * R 2 ) * √ ((R 1 - R 2 ) 2 + h 2 )]
Hemisphäre Oberfläche
- .
Gebogene Oberfläche = 2πr 2
Basisoberfläche = πr 2
Gesamtfläche = (2πr 2 ) + (πr 2 ) = 3πr 2
Rechteckige Prismenoberfläche
- .
Oberfläche = 2 (lw + lh + wh)
Pyramide-Oberfläche
- .
Seitliche Oberfläche = A√ (a 2 + 4h 2 )
Grundfläche = A 2
Gesamtoberfläche
= L + b = a 2 + a√ (a 2 + 4h 2 ))
= a (a + √ (a 2 + 4h 2 ))
Kugelförmige Oberfläche
- .
Oberfläche = 2πrh
Kugeloberfläche
- Oberfläche = 4πr 2
Zum Beispiel zur Kugel, wenn r = 3
- .
Um den Oberflächenbereich einer Kugel zu berechnen, verwenden Sie die folgende Formel: 4πr 2 . Wenn Sie R für seinen Wert ersetzt, erhalten Sie 4π * 3 2 , was 113.09734 m 2 entspricht.
Zum Beispiel zum Kegel, wenn r = 3, h = 3
- .
Um die Oberfläche eines Kegels zu berechnen, verwenden Sie die folgende Formel: πr (R + √ (R 2 + H 2 )). Wenn Sie R und H für ihre Werte ersetzen, erhalten Sie π3 (3 + * radic; (3 2 + 3 2 )), die 68,26028 m 2 entspricht .
Sprachauswahl:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.