Fester Volumenrechner |
| a = | |
| r = | |
| Units: | |
| Volume = | 0 |
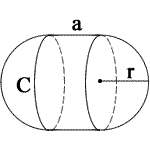
a = side length
r = radius
Kreiskegelvolumen & Oberfläche
- .
Volumen = (1/3) πr 2 h
Kapselvolumen
- .
Volumen = πr 2 ((4/3) r + a)
Kreiszylindervolumen.
- .
Volumen = πr 2 h
Würfelvolumen
- .
Volumen = A 3
Konisches Krupftum
- .
Volumen = (1/3) πH (R 1 2 2 2 + (r 1 * r 2 ))
Pyramid-Volumen.
- .
Volumen = (1/3) a 2 h
Hemisphäre Volumen.
- .
Volumen = (2/3) πr 3
Kugelkappenvolumen.
- .
Volumen = (1/3) πH 2 (3R - H)
Rechteckiges Prismenvolumen.
- .
Volumen = lwh.
Kugelvolumen.
- .
Volumen = (4/3) πr 3
Zum Beispiel zur Kapsel, wenn a = 2, r = 1
- .
Verwenden Sie zur Berechnung der Oberfläche einer Kapsel mit der folgenden Formel: 2πr (2R + A). Wenn Sie R und A für ihre Werte ersetzen, erhalten Sie 2π1 (2 * 1 + 2), was 25.13274 m 2 entspricht.
Zum Beispiel zur Hemisphäre, wenn r = 2
- .
Verwenden Sie zur Berechnung der Oberfläche einer Kapsel mit der folgenden Formel: 2πr (2R + A). Wenn Sie R und A für ihre Werte ersetzen, erhalten Sie 2π1 (2 * 1 + 2), was 25.13274 m 2 entspricht.
Sprachauswahl:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.