Volumen des Tetrahedron- / Parellelpiped-Rechners

Enter the vertex P ,,
Enter the vertex Q ,,
Enter the vertex R ,,
Enter the vertex S ,,
 
Volume of Parellelepiped
Volume of Tetrahedron

Volumen der Tetrahedron-Formel

Das Volumen eines Tetrahedrons ist 1/3 (Bereich der Basis) * Höhe

Wenn das Tetrahedron mit Scheitelpunkte A = (A1, A2, A3), B = (B1, B2, B3), C = (c1, c2, c3), und d = (d1, d2, d3) ist, ist das Volumen (d1, d2, d3) (d1, d2, d3) ( 1/6) · | det (A - D, B - D, C - D) |

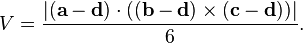
Volumen des Tetrahedron- / Parellelpiped-Rechners
Empfehlung Taschenrechner Luftgeschwindigkeitslöser erfassen Gallonen pro Stunde Kraftstoffrechner Fließwandlerrechner Luftkanalflussrechner Wärmerückgewinnungsrechner Volumeneinheit-Konverter Drehmoment zum PS-Konverter Windleistungsrechner Hydraulikdurchmesser Solver. Rauschkriteriumrechner Geschwindigkeitsumrichter Luftkanal-Velocity-Rechner Luftstromkopfverlustrechner Kapazität des Erdgasrohrs Rechner Elektromotorenrechner